In most undergraduate courses, groups are first introduced as a primarily algebraic concept – a ready equipped with a number of algebraic operations (group multiplication, multiplicative changed, and multiplicative identity) and obeying a number of rules of algebra (most notably the associative police). Information technology is but somewhat later on that ane learns that groups are not solely an algebraic object, but can also be equipped with the structure of a manifold (giving rising to Lie groups) or a topological infinite (giving rise to topological groups). (See also this post for a number of other ways to recollect almost groups.)

Another important way to enrich the structure of a group {G} is to give it some geometry. A fundamental way to provide such a geometric structure is to specify a listing of generators {S} of the group {G}. Permit united states of america call such a pair {(G,S)} a generated group; in many of import cases the set of generators {S} is finite, leading to a finitely generated grouping. A generated group {(G,S)} gives rise to the word metric {d: G \times G \rightarrow {\bf N}} on {G}, defined to be the maximal metric for which {d(x,sx) \leq 1} for all {x \in G} and {s \in S} (or more explicitly, {d(x,y)} is the least {m} for which {y = s_1^{\epsilon_1} \ldots s_m^{\epsilon_m} x} for some {s_1,\ldots,s_m \in S} and {\epsilon_1,\ldots,\epsilon_m \in \{-1,+1\}}). This metric and then generates the balls {B_S(R) := \{ x \in G: d(x,\hbox{id}) \leq R \}}. In the finitely generated case, the {B_S(R)} are finite sets, and the charge per unit at which the cardinality of these sets grow in {R} is an important topic in the field of geometric group theory. The idea of studying a finitely generated group via the geometry of its metric goes dorsum at least to the work of Dehn.

I mode to visualise the geometry of a generated grouping is to look at the (labeled) Cayley colour graph of the generated group {(G,S)}. This is a directed coloured graph, with edges coloured by the elements of {S}, and vertices labeled by elements of {G}, with a directed border of color {s} from {x} to {sx} for each {x \in G} and {s \in S}. The word metric then corresponds to the graph metric of the Cayley graph.

For instance, the Cayley graph of the cyclic grouping {{\bf Z}/6{\bf Z}} with a single generator {S = \{1\}} (which we draw in dark-green) is given as

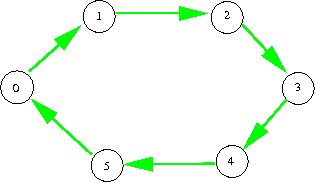
while the Cayley graph of the same group but with the generators {S = \{2,3\}} (which we draw in blueish and ruby respectively) is given as

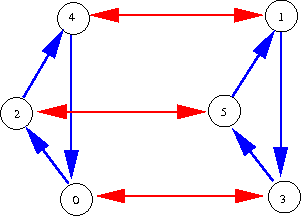
Nosotros can thus see that the same group can have somewhat different geometry if i changes the prepare of generators. For instance, in a large cyclic group {{\bf Z}/N{\bf Z}}, with a single generator {S = \{1\}} the Cayley graph "looks one-dimensional", and assurance {B_S(R)} grow linearly in {R} until they saturate the entire group, whereas with two generators {S = \{s_1,s_2\}} chosen at random, the Cayley graph "looks two-dimensional", and the balls {B_S(R)} typically grow quadratically until they saturate the entire grouping.

Cayley graphs have three distinguishing properties:

It is easy to verify that a directed coloured graph is a Cayley graph (up to relabeling) if and merely if it obeys the above three properties. Indeed, given a graph {(V,E)} with the above properties, ane sets {G} to equal the (coloured) automorphism group of the graph {(V,E)}; arbitrarily designating i of the vertices of {V} to exist the identity element {\hbox{id}}, nosotros tin then identify all the other vertices in {V} with a group chemical element. 1 then identifies each colour {s \in S} with the vertex that one reaches from {\hbox{id}} by an {s}-coloured edge. Conversely, every Cayley graph of a generated group {(G,S)} is clearly regular, is connected considering {S} generates {G}, and has isomorphisms given by right multiplication {x \mapsto xg} for all {g\in G}. (The regularity and connexion properties already ensure the uniqueness component of the homogeneity property.)

From the above equivalence, we encounter that we practice not really need the vertex labels on the Cayley graph in order to describe a generated group, and so we volition now drop these labels and work solely with unlabeled Cayley graphs, in which the vertex set is not already identified with the group. As we saw in a higher place, one merely needs to designate a marked vertex of the graph as the "identity" or "origin" in order to plough an unlabeled Cayley graph into a labeled Cayley graph; but from homogeneity we see that all vertices of an unlabeled Cayley graph "look the same" and in that location is no approved preference for choosing one vertex every bit the identity over another. I prefer hither to keep the graphs unlabeled to emphasise the homogeneous nature of the graph.

It is instructive to revisit the bones concepts of group theory using the language of (unlabeled) Cayley graphs, and to see how geometric many of these concepts are. In social club to facilitate the cartoon of pictures, I work here just with small finite groups (or Cayley graphs), but the give-and-take certainly is applicable to large or infinite groups (or Cayley graphs) also.

For case, in this setting, the concept of abelianness is analogous to that of a apartment (cypher-curvature) geometry: given any two colours {s_1, s_2}, a directed path with colours {s_1, s_2, s_1^{-1}, s_2^{-1}} (adopting the obvious convention that the reversal of an {s}-coloured directed edge is considered an {s^{-1}}-coloured directed border) returns to where it started. (Note that a generated group {(G,S)} is abelian if and only if the generators in {S} pairwise commute with each other.) Thus, for instance, the two depictions of {{\bf Z}/6{\bf Z}} above are abelian, whereas the group {S_3}, which is also the dihedral group of the triangle and thus admits the Cayley graph

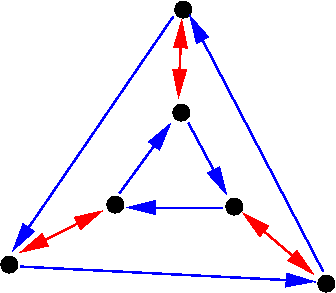
is not abelian.

A subgroup {(G',S')} of a generated group {(G,S)} tin exist easily described in Cayley graph language if the generators {S'} of {G'} happen to exist a subset of the generators {S} of {G}. In that instance, if one begins with the Cayley graph of {(G,S)} and erases all colours except for those colours in {S'}, so the graph foliates into continued components, each of which is isomorphic to the Cayley graph of {(G',S')}. For instance, in the higher up Cayley graph depiction of {S_3}, erasing the blue colour leads to iii copies of the red Cayley graph (which has {{\bf Z}/2{\bf Z}} as its construction group), while erasing the red color leads to two copies of the blueish Cayley graph (which as {A_3 \equiv {\bf Z}/3{\bf Z}} as its construction group). If {S'} is not independent in {S}, then one has to first "alter ground" and add or remove some coloured edges to the original Cayley graph earlier ane can obtain this formulation (thus for instance {S_3} contains two more subgroups of order two that are not immediately apparent with this choice of generators). However the geometric intuition that subgroups are analogous to foliations is even so quite a good one.

Nosotros saw that a subgroup {(G',S')} of a generated group {(G,S)} with {S' \subset S} foliates the larger Cayley graph into {S'}-continued components, each of which is a re-create of the smaller Cayley graph. The remaining colours in {S} then bring together those {S'}-components to each other. In some cases, each colour {s \in S\backslash S'} will connect a {S'}-component to exactly 1 other {S'}-component; this is the case for instance when one splits {S_3} into two blue components. In other cases, a colour {s} can connect a {S'}-component to multiple {S'}-components; this is the instance for instance when one splits {S_3} into three red components. The former case occurs precisely when the subgroup {G'} is normal. (Note that a subgroup {G'} of a generated group {(G,S)} is normal if and simply if left-multiplication by a generator of {S} maps right-cosets of {G'} to right-cosets of {G'}.) Nosotros can then quotient out the {(G',S')} Cayley graph from {(G,S)}, leading to a quotient Cayley graph {(G/G', S \backslash S')} whose vertices are the {S'}-connected components of {(G,S)}, and the edges are projected from {(G,S)} in the obvious way. We tin can so view the original graph {(G,S)} as a bundle of {(G',S')}-graphs over a base of operations {(G/G',S\backslash S')}-graph (or equivalently, an extension of the base graph {(G/G',S\backslash S')} by the fibre graph {(G',S')}); for instance {S_3} can exist viewed equally a bundle of the bluish graph {A_3} over the red graph {{\bf Z}/2{\bf Z}}, but not conversely. We thus meet that the geometric analogue of the concept of a normal subgroup is that of a bundle. The generators in {S \backslash S'} can be viewed as describing a connection on that package.

Annotation, though, that the construction group of this connection is not simply {G'}, unless {G'} is a central subgroup; instead, it is the larger group {G' \rtimes \hbox{Aut}(G')}, the semi-direct product of {G'} with its automorphism grouping. This is because a non-central subgroup {G'} can exist "twisted around" past operations such as conjugation {g' \mapsto sg's^{-1}} by a generator {s \in S}. And so central subgroups are coordinating to the geometric notion of a principal packet. For instance, here is the Heisenberg grouping

\displaystyle \begin{pmatrix} 1 & {\bf F}_2 & {\bf F}_2 \\ 0 & 1 & {\bf F}_2 \\ 0 & 0 & 1 \end{pmatrix}

over the field {{\bf F}_2} of two elements, which one can view equally a central extension of {{\bf F}_2^2} (the blue and green edges, afterwards quotienting) by {{\bf F}_2} (the carmine edges):

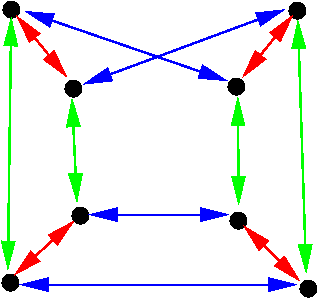
Note how shut this group is to being abelian; more generally, one can call back of nilpotent groups as being a slight perturbation of abelian groups.

In the case of {S_3} (viewed equally a parcel of the blue graph {A_3} over the blood-red graph {{\bf Z}/2{\bf Z}}), the base graph {{\bf Z}/2{\bf Z}} is in fact embedded (three times) into the large graph {S_3}. More than generally, the base of operations graph {(G/G', S \backslash S')} tin be lifted back into the extension {(G,S)} if and just if the brusk verbal sequence {0 \rightarrow G' \rightarrow G \rightarrow G/G' \rightarrow 0} splits, in which case {G} becomes a semidirect product {G \equiv G' \rtimes H} of {G'} and a lifted copy {H} of {G/G'}. Non all bundles tin exist carve up in this fashion. For case, consider the grouping {{\bf Z}/9{\bf Z}}, with the blue generator {1} and the red generator {3}:

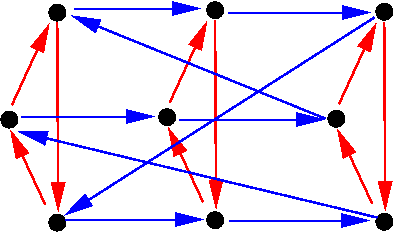
This is a {{\bf Z}/3{\bf Z}}-bundle over {{\bf Z}/3{\bf Z}} that does not separate; the blueish Cayley graph of {{\bf Z}/3{\bf Z}} is not visible in the {{\bf Z}/9{\bf Z}} graph directly, merely only afterwards one quotients out the cerise fibre subgraph. The notion of a splitting in group theory is coordinating to the geometric notion of a global gauge. The being of such a splitting or approximate, and the human relationship between two such splittings or gauges, are controlled past the group cohomology of the sequence {0 \rightarrow G' \rightarrow G \rightarrow G/G' \rightarrow 0}.

Even when one has a splitting, the package need non be completely trivial, considering the bundle is non principal, and the connection can still twist the fibres effectually. For instance, {S_3} when viewed as a packet over {{\bf Z}/2{\bf Z}} with fibres {A_3} splits, but observe that if one uses the ruby-red generator of this splitting to move from one copy of the bluish {A_3} graph to the other, that the orientation of the graph changes. The bundle is trivialisable if and only if {G'} is a direct summand of {G}, i.e. {G} splits equally a direct product {G = G' \times H} of a lifted copy {H} of {G/G'}. Thus we run into that the geometric analogue of a direct summand is that of a trivialisable bundle (and that niggling bundles are and then the counterpart of direct products). Note that there can be more than one manner to trivialise a package. For instance, with the Klein four-group {{\bf Z}/2{\bf Z} \times {\bf Z}/2{\bf Z}},

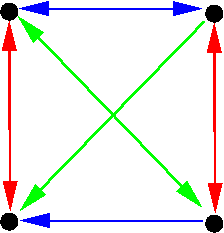
the crimson fibre {{\bf Z}/2{\bf Z}} is a direct summand, merely i can use either the blue elevator of {{\bf Z}/2{\bf Z}} or the green lift of {{\bf Z}/2{\bf Z}} as the complementary factor.